Question

The length of a rectangle is one less than twice its width. The area is 66 square centimeters. Find the length and width.

Answer 1

I. Length, L = 11 cm

II. Width, W = 6 cm

Explanation:

Let the length of the rectangle be L.

Let the width of the rectangle be W.

Given the following data;

Area of rectangle = 66 cm²

Translating the word problem into an algebraic expression, we have;

L = 2W - 1 .....equation 1

We know that the area of a rectangle is given by the formula;

A = L * W

Substituting

66 = L * W ....equation 2

Substituting eqn 1 into eqn 2, we have;

66 = (2W - 1) * W

66 = 2W² - W

2W² - W - 66 = 0

Note: the standard form of a quadratic equation is ax² + bx + c = 0

a = 2, b = -1 and c = -66

Solving the quadratic equation using the quadratic formula;

The quadratic equation formula is;

`x = \frac {-b \; \pm \sqrt {b^(2) - 4ac}}{2a}`

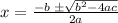
Substituting into the equation, we have;

`x = \frac {-(-1) \; \pm \sqrt {1^(2) - 4*2*(-66)}}{2*2}`

`x = \frac {1 \pm \sqrt {1 - (-528)}}{4}`

`x = \frac {1 \pm \sqrt {1 + 528}}{4}`

`x = \frac {1 \pm \sqrt {529}}{4}`

`x = \frac {1 \pm 23}{4}`

`x_(1) = \frac {1 + 23}{4}`

`x_(1) = \frac {24}{4}`

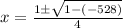
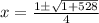
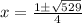
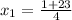
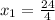
x1 = 6

We do not need the negative value of x, so we proceed.

Therefore, Width, W = x1 = 6 cm

Next, we find the length L;

From eqn 1;

L = 2W - 1

L = 2(6) - 1

L = 12 - 1

L = 11 cm