Answer:
The two consecutive integers are 6 and 8 or -8 and -6.
Explanation:
The product of two consecutive even integers is 48, and we want to find the two integers.
We will let x represent the first even integer.
Then the consecutive even integer will be (x + 2).
Its product is 48. Therefore:
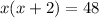
Solve for x. Since this is a quadratic, we should get one side to equal to 0. Expand:
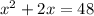
Subtract 48 from both sides:
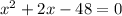
Factor:
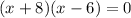
Zero Product Property:
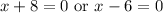
Solve for each case:
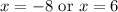
Therefore, our two consecutive integers are 6 and 8 or -8 and -6.