Question

plz hurry!! A person standing close to the edge on top of a 108-foot building throws a ball vertically upward. The quadratic function h ( t ) = − 16 t 2 + 132 t + 108 h ( t ) = - 16 t 2 + 132 t + 108 models the ball's height above the ground, h ( t ) h ( t ) , in feet, t t seconds after it was thrown. a) What is the maximum height of the ball?

Answer 1

The maximum height of the ball is 380.25 feet in the air.

Explanation:

The quadratic function:

`h(t)=-16t^2+132t+108`

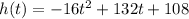
Models the ball's height h(t), in feet, above the ground t seconds after it was thrown.

We want to determine the maximum height of the ball.

Note that this is a quadratic function. Therefore, the maximum or minimum value will always occur at its vertex point.

Since our leading coefficient is leading, we have a maximum point. So to find the maximum height, we will find the vertex. The vertex of a quadratic equation is given by:

`\displaystyle \left(-(b)/(2a),f\left((b)/(2a)\right)\right)`

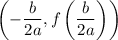
In this case, a = -16, b = 132, and c = 108. Find the t-coordinate of the vertex:

`\displaystyle t=-(132)/(2(-16))=-(132)/(-32)=(33)/(8)=4.125`

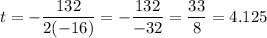
So, the maximum height occurs after 4.125 seconds of the ball being thrown.

To find the maximum height, substitute this value back into the equation. Thus:

`h(4.125)=-16(4.125)^2+132(4.125)+108=380.25\text{ feet}`

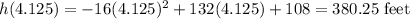
The maximum height of the ball is 380.25 feet in the air.