Question

What is the % dissociation of a solution of acetic acid if at equilibrium the solution has a pH = 4.74 and a pKa = 4.74?

Answer 1

`\% diss = 50\%`

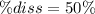
Step-by-step explanation:

Hello there!

In this case, when considering weak acids which have an associated percent dissociation, we first need to set up the ionization reaction and the equilibrium expression:

`HA\rightleftharpoons H^++A^-\\\\Ka=([H^+][A^-])/([HA])`

Now, by introducing x as the reaction extent which also represents the concentration of both H+ and A-, we have:

`Ka=(x^2)/([HA]_0-x) =10^(-4.74)=1.82x10^(-5)`

Thus, it is possible to find x given the pH as shown below:

`x=10^(-pH)=10^(-4.74)=1.82x10^(-5)M`

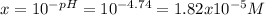
So that we can calculate the initial concentration of the acid:

`((1.82x10^(-5))^2)/([HA]_0-1.82x10^(-5)) =1.82x10^(-5)\\\\(1.82x10^(-5))/([HA]_0-1.82x10^(-5)) =1\\\\`

`[HA]_0=3.64x10^(-5)M`

Therefore, the percent dissociation turns out to be:

`\% diss=(x)/([HA]_0)*100\% \\\\\% diss=(1.82x10^(-5)M)/(3.64x10^(-5)M)*100\% \\\\\% diss = 50\%`

Best regards!