Answer:
10√6 ; √5/6 ; 42√14
Explanation:
1) - factorise 240
240/ 2 = 120
120/2 = 60
60/2 = 30
30/2 = 15
15/3 = 5
5/5 = 1
240 = 2^4 * 3 * 5
- simplify
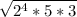 . We can in particular simplify
. We can in particular simplify
 by dividing the index of the radius and the exponent by 2
by dividing the index of the radius and the exponent by 2
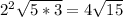
- factorise 12
12/2 =.6
6/2 = 3
3/3 = 1
12 = 2^2 * 3
- simplify
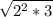
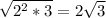
- divide
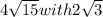
number : number = 4/2 = 2
square : square = √15 / √3 = √5
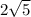
- multiply √30 with 2√5
number x number = 2x1 = 2
square x square = √30 x √5 = √150
2√150
- factorize 150
150/ 2 = 75
75/3 = 25
25/5 = 5
5/5 = 1
150 = 5^2 x 2 x 3
- simplify

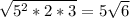
- multiply 2 and 5
10√6
2) remember that a division of two terms with the same square can be rewrite as
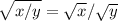
- rewrite the expression in this way
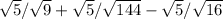
- solve the squares of the denominators
√5/3 + √5/12 -√5/4
- rewrite the fraction with the same denominator = 12
(4√5 + √5 - 3√5)/12
- simplify the numerators by sum the numbers
2√5/12
- divide 2 and 12
√5/6
3)
- multiply 3√2 and √14
number x number = 3 x 1 = 3
square x square = √2 x √14 = √28
3√28
- factorise 28
28 = 2^2 x 7
- simplify
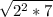
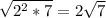
- multiply 3 and 2
6√7
- factorise 98
98/2 = 49
49/7 = 7
7/7 = 1
98 = 7^2 * 2
- simplify
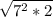
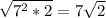
- multiply 6√7 and 7√2
number x number = 42
square x square = √14
42√14