Question

Find the degree of –5w3 – 4w2 + 7w + 16.
A. –5
B. 16
C. 14
D. 3

Answer 1

The answer you are looking for is 3

Answer 2

The degree of the polynomial is 3. Therefore, the correct option is D.

In algebra, the degree of a polynomial is the highest power of the variable (or variables) in the polynomial. The degree provides information about the behavior of the polynomial, particularly its end behavior. For a polynomial in one variable, the degree is determined by looking at the exponent of the term with the highest power.

Let's look at the polynomial
`\(-5w^3 - 4w^2 + 7w + 16\)`:

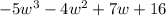1. The term
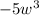`\(-5w^3\)` has a degree of 3 because the variable
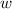`\(w\)` is raised to the power of 3.

2. The term
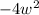`\(-4w^2\)` has a degree of 2 because the variable
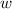`\(w\)` is raised to the power of 2.

3. The term
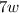`\(7w\)` has a degree of 1 because the variable
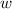`\(w\)` is raised to the power of 1.

4. The term
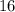`\(16\)` can be considered as
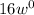`\(16w^0\)`, and it has a degree of 0.

The degree of the polynomial is the highest degree among its terms, which is 3 in this case. Therefore, the given polynomial
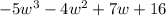`\(-5w^3 - 4w^2 + 7w + 16\)` is a third-degree polynomial.

In general, the degree of a polynomial is the highest power to which the variable is raised in any term of the polynomial. For example:

-
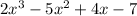`\(2x^3 - 5x^2 + 4x - 7\)` is a third-degree polynomial.

-
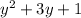`\(y^2 + 3y + 1\)` is a second-degree polynomial.

-
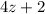`\(4z + 2\)` is a first-degree polynomial (linear).

Understanding the degree of a polynomial is important because it helps us classify and analyze polynomials, and it provides information about their behavior as
`\(x\)` (or any other variable) becomes very large or very small.