Question

A rectangle is fenced off for a robot competition. The dimensions of the competition area are 35 feet by 25 feet. To help track the robots, the southwest vertex of the rectangle is assigned coordinates (0, 0) and the northeast vertex is assigned coordinates (35, 25). The robot that traveled from (3, 18) and moved in a linear path for 5 seconds. After 5 seconds, the robot’s position was at (31, 6). What is the approximate speed of the robot during the 5 seconds? Give your answer to the nearest whole number.

Answer 1

The approximate speed of the robot during the 5 seconds is:

• 6 ft/s

Explanation:

To calculate the speed of the robot, you must begin with the positions, the first position (3, 18) and the second position (31, 6), you can see, in the height it moved from 3 to 31, it means 28 feet, in the width it moves from 18 to 6, it means 12 feet, with these data you can construct a triangle where you have the opposite leg and adjacent leg, now you must calculate the hypotenuse, because it is the linear path from the first position to the second position that the robot took, for this, you can use the Pythagoras theorem:

• 
  `hypotenuse^(2)` =
  `opposite leg^(2)` +
  `adjacent leg^(2)`
• 
  `hypotenuse^(2)` =
  `12^(2) +28^(2)`
• 
  `hypotenuse=\sqrt{ 12^(2)+28^(2) }`
• 
  `hypotenuse=30.46 ft`

With the value of the distance traveled, and the time used (5 seconds), we can calculate the speed with the next formula:

• 
  `Speed =(distance)/(time)`
• 
  `Speed = (30.46 ft)/(5 s)`
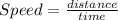
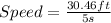
• Speed = 6.09 ft/s

As you need the speed in the nearest whole number, then:

• Speed = 6 ft/s