Question

A box contains 5 red, 4 white and 6 blue balls. If three balls are drawn at random without replacement, determine the probability that none of the balls selected is red.

Answer 1

The probability that none of the balls selected is red ²⁴/₉₁

Explanation:

Given;

number of red balls, R = 5

number of white balls, W = 4

number of blue balls, B = 6

Total number of balls, = 5 + 4 + 6 = 15

Probability of selecting 3 none red balls = P(WWW) or P(BBB) or P(WWB) or P(WBW) or P(BWW) or P(BBW) or P(BWB) or P(WBB)

`P = ((4)/(15) * (3)/(14) * (2)/(13) ) + ((6)/(15) * (5)/(14) * (4)/(13) ) + ((4)/(15) * (3)/(14) * (6)/(13) ) + ((4)/(15) * (6)/(14) * (3)/(13) ) + \\\\((6)/(15) * (4)/(14) * (3)/(13) ) + ((6)/(15) * (5)/(14) * (4)/(13) ) + ((6)/(15) * (4)/(14) * (5)/(13) ) + ((4)/(15) * (6)/(14) * (5)/(13) )`

`P = (24)/(2730) + (120)/(2730) + (72)/(2730) +(72)/(2730) + (72)/(2730) + (120)/(2730) + (120)/(2730) + (120)/(2730) \\\\P = (720)/(2730) \\\\P = (24)/(91) \\\\`

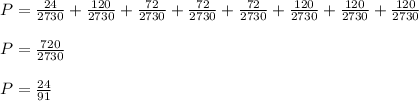
Therefore, the probability that none of the balls selected is red ²⁴/₉₁