Question

Pls help, simple, and not that hard

Answer 1

Answer: A) None of the above

==================================================

Step-by-step explanation:

Let's solve (x-2)(x-5) = 0 and doing so leads to x = 2 or x = 5. Plugging either value in for x makes the expression (x-2)(x-5) become 0.

Let's pick a value to the left of x = 2, let's say we pick x = 0. Plug this into the expression (x-2)(x-5) and we get the following:

(x-2)(x-5)

(0-2)(0-5)

(-2)(-5)

10

The result is a positive number, meaning that (x-2)(x-5) is positive when we select a value smaller than 2.

Now we'll repeat this with a value between 2 and 5. Let's say we pick on x = 3.

So,

(x-2)(x-5)

(3-2)(3-5)

(1)(-2)

-2

The result is negative, so (x-2)(x-5) is negative when 2 < x < 5. This immediately rules out choices C and E.

Unfortunately, answer choices B and D won't work either for similar reasoning. The only thing left is choice A.

Side note: The answer in interval notation is
`(-\infty, 2] \cup [5, \infty)` so basically it's everything but values between 2 and 5; however, x = 2 and x = 5 are part of the solution set.

Another side note: if you flip the inequality sign from
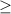`\ge` to
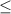`\le`, then the answer would be choice C.