2 Answers

Nicolast · Answer 1 · 2022-11-26T19:42:07+0000

The solution to the inequality is option D:
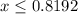$x \leq 0.8192$ . Rounded to the nearest ten-thousandth, this is approximately 0.8192.

To solve the inequality
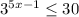$3^(5 x-1) \leq 30$ , we can follow these steps:

Take the logarithm (base 3) of both sides to eliminate the exponent:

$5 x-1 \leq \log _3(30)$

Solve for x:

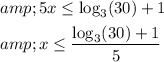
$\begin{aligned}& 5 x \leq \log _3(30)+1 \\& x \leq (\log _3(30)+1)/(5)\end{aligned}$

Now, we can calculate the numerical value for x:

$x \leq (\log _3(30)+1)/(5) \approx 0.8192$

So, the correct answer is D.

Please log in or register to add a comment.