Question

A pond has 150 fish and the population decreases by 8% each day. How many days before there are 30 fish

Answer 1

19 days

Explanation:

Given

`a = 150` --- initial

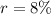`r = 8\%` -- rate

Required

Days when the fish gets to 30

The function is exponential and as such it follows;

`y = ab^x`

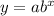
Where x represents the number of days and y the number of fishes

Because the fishes decreases;

`b = 1 - r`

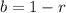
So, we have:

`b = 1 - 8\%`

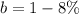
Express as decimal

`b = 1 - 0.08`

`b = 0.92`

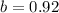
In
`y = ab^x`

`a =150`

`y = 30`

`b = 0.92`

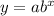
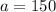
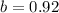
So, we have:

`30 = 150 * 0.92^x`

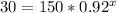
Divide both sides by 150

`0.2 = 0.92^x`

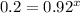
Take log of both sides

`log(0.2) = log(0.92^x)`

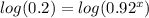
Apply law of logarithm

`log(0.2) = x\ log(0.92)`

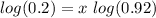
Make x the subject

`x = (log(0.2))/(log(0.92))`

`x = (-0.6990)/(-0.0362)`

`x = 19.309`

`x \approx 19`

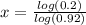
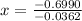
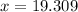
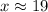
Hence, it takes approximately 19 days