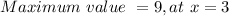Based on the extreme value theorem, what is the maximum value of f(x) = –x2 + 6x over the interval [1, 4]?

Question

asked Aug 2, 2022 152k views

2 Answers

RedZ · Answer 1 · 2022-08-06T10:15:10+0000

Answer:

$Maximum\ value\ =9 ,at\ x=3$

Explanation:

From the question we are told that:

Function given

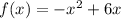
f(x) = -x^2 + 6x

Co-ordinates

(x,y)=[1, 4]

Generally the second differentiation of function is mathematically given by

-2x+6

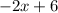
Therefore critical point

x=3

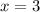
Generally the substitutions of co-ordinate into function is mathematically given by

For 1

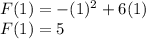
$F(1)=-(1)^2 + 6(1)\\F(1)=5$

For 4

$F(4)=-(4)^2 + 6(4)\\F(4)=8$

For critical point 3

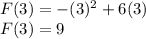
$F(3)=-(3)^2 + 6(3)\\F(3)=9$

Therefore the maximum value of f(x) = –x2 + 6x over the interval [1, 4] is given by

$Maximum\ value\ =9 ,at\ x=3$