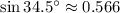Answer:
a)
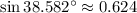 , b)
, b)
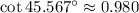 , c)
, c)
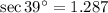 , d)
, d)
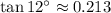 , e)
, e)
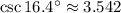 , f)
, f)
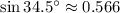
Explanation:
Sabemos que un minuto equivale a
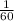 de un grado sexagesimal, mientras que un segundo equivale a
de un grado sexagesimal, mientras que un segundo equivale a
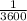 de un grado sexagesimal, entonces procedemos a convertir cada ángulo a su forma decimal y simplificamos en términos de senos y cosenos mediante identidades trigonométricas:
de un grado sexagesimal, entonces procedemos a convertir cada ángulo a su forma decimal y simplificamos en términos de senos y cosenos mediante identidades trigonométricas:
a)
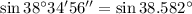
Por tablas trigonométricas tenemos que
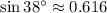 y
y
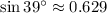 , mediante interpolación lineal tenemos que:
, mediante interpolación lineal tenemos que:
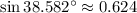
b)
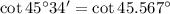
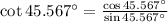
Por tablas trigonométricas tenemos que
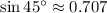 ,
,
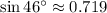 ,
,
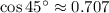 y
y
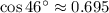 , mediante interpolación lineal tenemos que:
, mediante interpolación lineal tenemos que:
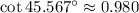
c)
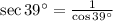
Por tablas trigonométricas tenemos que
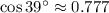 , entonces tenemos que:
, entonces tenemos que:
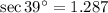
d)
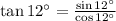
Por tablas trigonométricas tenemos que
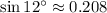 and
and
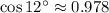 , entonces tenemos que:
, entonces tenemos que:
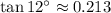
e)
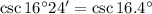
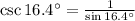
Por tablas trigonométricas tenemos que
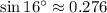 y
y
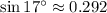 , mediante interpolación lineal tenemos que:
, mediante interpolación lineal tenemos que:
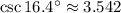
f)
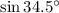
Por tablas trigonométricas tenemos que
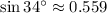 y
y
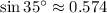 , mediante interpolación lineal tenemos que:
, mediante interpolación lineal tenemos que: