Answer:
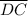 = 7
= 7
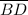 = √35
= √35
 = 2·√15
= 2·√15
Explanation:
Please find attached the drawing of right triangle ABC created with MS Visio
Let 'x' represent
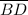 let 'y' represent
let 'y' represent
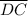 , and let 'z' represent
, and let 'z' represent
 , we get;
, we get;
5² + x² = z²...(1)
x² + y² = (2·√21)² = 84
x² + y² = 84...(2)
84 + z² = (5 + y)²...(3)
From equation (1), we have;
x² = z² - 5²...(4)
From equation (2), and equation (4), we have;
x² + y² = 84 = (z² - 5²) + y² = 84
∴ z² = 84 - y² + 5² = 109 - y²
z² = 109 - y²...(5)
From equation (3), and equation (5), we have;
84 + z² = (5 + y)² = 84 + (109 - y²) = (5 + y)²
84 + (109 - y²) = (5 + y)²
(5 + y)² - (84 + (109 - y²)) = 0
2·y² + 10·y - 168 = 0
y² + 5·y - 84 = 0
y = (-5 ± √(5² - 4 × 1 × (-84)))/(2 × 1)
y = 7, or y = -12
We note that 'y' is a natural number, therefore, the correct option of the two options is y = 7
y =
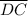 = 7
= 7
From equation (2), we have;
x² + y² = 84
x² = 84 - y² = 84 - 7² = 35
x = √35
x =
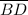 = √35
= √35
z² = 109 - y²
∴ z² = 109 - 7² = 60
z = √60 = 2·√15
z = 2·√15
z =
 = 2·√15.
= 2·√15.