Answer:
There will be 729 daffodils in the sixth week
Explanation:
Given
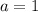 --- start
--- start
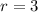 --- weekly rate
--- weekly rate
Required
Number of daffodils in 6th week
This question illustrates an exponential function which is represented as
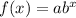
Where
f(x) = Number of daffodils at x week
x = The week
a = Initial number of daffodils
b= rate
So, we have:
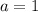

Hence:
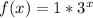

At the 6th week
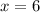
So:
 ---- as a power
---- as a power
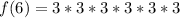 --- related multiplication
--- related multiplication
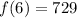 --- standard form
--- standard form