Question

On a coordinate plane, parallelograms A B C D and E F G H are shown. Parallelogram A B C D has points (4, 2), (7, 2), (4, 6), (1, 6). Parallelogram E F G H has points (negative 2, 2), (negative 5, 2), (negative 6, 6), and (negative 3, 6). How do the areas of the parallelograms compare? The area of parallelogram ABCD is 4 square units greater than the area of parallelogram EFGH. The area of parallelogram ABCD is 2 square units greater than the area of parallelogram EFGH. The area of parallelogram ABCD is equal to the area of parallelogram EFGH. The area of parallelogram ABCD is 2 square units less than the area of parallelogram EFGH.

Answer 1

C)

Explanation:

e2020

Answer 2

The area of parallelogram ABCD is equal to the area of parallelogram EFGH.

Explanation:

Given

Parallelogram ABCD

`A = (4,2)`

`B = (7,2)`

`C =(4,6)`

`D = (1,6)`

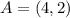
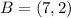
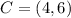
Parallelogram EFGH

`E =(-2,2)`

`F = (-5,2)`

`G = (-6,6)`

`H = (-3,6)`

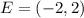
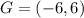
Required

Compare the areas of both parallelograms

The area of a parallelogram is:

`Area =Base * Height`

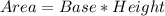
So: To do this, we plot ABCD and EFGH on a grid, then we measure the base and the height of both.

See attachment 1 for ABCD

In (1), we have:

`Base = 3\ units`

`Height = 4\ units`

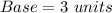
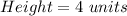
So, the area is:

`A_1 = 3 * 4`

`A_1 = 12`

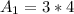
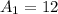
See attachment 2 for EFGH

In (2), we have:

`Base = 3\ units`

`Height = 4\ units`

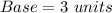
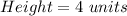
So, the area is:

`A_2 = 3 * 4`

`A_2 = 12`

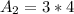
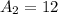
By comparison, they both have the same areas