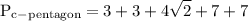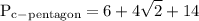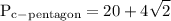Question

Please for the love of god anwser my question lay correctly I really need your help :( I will give 25 points :)! This is geometry

I need help asap it's rn​

Answer 1

`\displaystyle \rm A_{ \text{c - pentagon}} =41`

`\rm \displaystyle P _( \rm c - pentagon) = 20+ 4 √(2)`

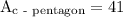
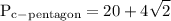
Explanation:

we have a square and a triangle

we want to figure out the area and the perimeter of the pentagon

to figure out the area of the pentagon we can use the given formula:

`\displaystyle \rm A_{ \text{c - pentagon}} = A_{ \text{squre}} - A_{ \text{triangle}}`

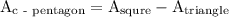
let's figure out
`A_(\rm square)`:

since the given shape is a square Every angle of its 90° Thus the triangle is a right angle triangle

therefore the height is 4

`\displaystyle A _( \rm triangle) = (1)/(2) * b * h`

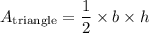
substitute h and b

`\displaystyle A _( \rm triangle) = (1)/(2) * 4 * 4`

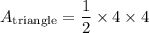
reduce fraction:

`\displaystyle A _( \rm triangle) = 2 * 4`

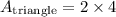
simplify multiplication:

`\displaystyle A _( \rm triangle) = 8`

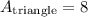
likewise square

`\displaystyle A _( \rm squre) = {s}^(2)`

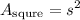
substitute s:

`\displaystyle A _( \rm squre) = {7}^(2)`

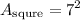
simplify square

`\displaystyle A _( \rm squre) = 49`

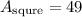
hence,

`\displaystyle \rm A_{ \text{c - pentagon}} =49- 8`

`\displaystyle \rm A_{ \text{c - pentagon}} =41`

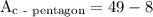
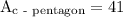
to figure out perimeter

let's figure out hypotenuse first

`\displaystyle h = \sqrt{ {4}^(2) + {4}^(2) }`

`\displaystyle h = √( 16 + 16)`

`\displaystyle h = 4 √(2)`

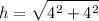
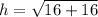
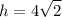
therefore,

`\rm \displaystyle P _( \rm c - pentagon) = 3 + 3 + 4 √(2) + 7 + 7`

`\rm \displaystyle P _( \rm c - pentagon) = 6 + 4 √(2) + 14`

`\rm \displaystyle P _( \rm c - pentagon) = 20+ 4 √(2)`