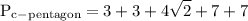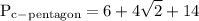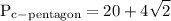Answer:
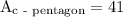
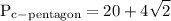
Explanation:
we have a square and a triangle
we want to figure out the area and the perimeter of the pentagon
to figure out the area of the pentagon we can use the given formula:
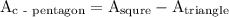
let's figure out
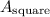 :
:
since the given shape is a square Every angle of its 90° Thus the triangle is a right angle triangle
therefore the height is 4
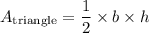
substitute h and b
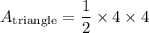
reduce fraction:
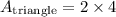
simplify multiplication:
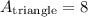
likewise square
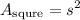
substitute s:
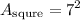
simplify square
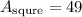
hence,
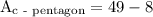
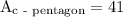
to figure out perimeter
let's figure out hypotenuse first
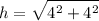
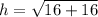
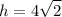
therefore,