Question

If the distance from A (5,6) to B (1, b) is twice the distance from B to

C(1, -3), determine the possible values of b.

Answer 1

The possible values of
`b` are -2.944 and -9.055, respectively.

Explanation:

From statement we know that
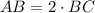`AB = 2\cdot BC`. By Analytical Geometry, we use the equation of a line segment, which is an application of the Pythagorean Theorem:

`AB = 2\cdot BC`

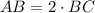
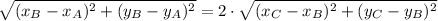`\sqrt{(x_(B)-x_(A))^(2)+(y_(B)-y_(A))^(2)} = 2\cdot \sqrt{(x_(C)-x_(B))^(2)+(y_(C)-y_(B))^(2)}` (1)

Where:

`x_(A)`,
`x_(B)`,
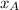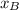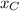`x_(C)` - x-Coordinates of points A, B and C.

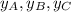`y_(A), y_(B), y_(C)` - y-Coordinates of points A, B and C.

`(x_(B)-x_(A))^(2)+(y_(B)-y_(A))^(2) = 4\cdot (x_(C)-x_(B))^(2)+4\cdot (y_(C)-y_(B))^(2)`

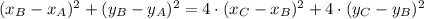
Then, we expand and simplify the expression above:

`x_(B)^(2)-2\cdot x_(A)\cdot x_(B) +x_(A)^(2) +y_(B)^(2)-2\cdot y_(A)\cdot y_(B) + y_(A)^(2) = 4\cdot (x_(C)^(2)-2\cdot x_(C)\cdot x_(B)+x_(B)^(2))+4\cdot (y_(C)^(2)-2\cdot y_(C)\cdot y_(B)+y_(B)^(2))`

`x_(B)^(2)-2\cdot x_(A)\cdot x_(B) + x_(A)^(2) +y_(B)^(2)-2\cdot y_(A)\cdot y_(B) + y_(A)^(2) = 4\cdot x_(A)^(2)-8\cdot x_(C)\cdot x_(B)+4\cdot x_(B)^(2)+4\cdot y_(C)^(2)-8\cdot y_(C)\cdot y_(B)+4\cdot y_(B)^(2)`

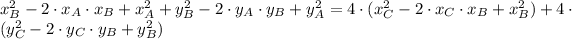
If we know that
`x_(A) = 5`,
`y_(A) = 6`,
`x_(B) = 1`,
`y_(B) = b`,
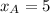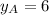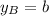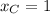`x_(C) = 1` and
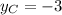`y_(C) = -3`, then we have the following expression:

`1 -10 +25 +b^(2) -12\cdot b+36 = 100 -8 +4 +36+24\cdot b +4\cdot b^(2)`

`b^(2)-12\cdot b +52 = 4\cdot b^(2)+24\cdot b +132`

`3\cdot b^(2)+36\cdot b +80 = 0`

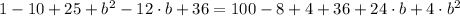
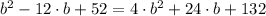
This is a second order polynomial, which means the existence of two possible real solutions. By Quadratic Formula, we have the following y-coordinates for point B:

`b_(1) \approx -2.944`,
`b_(2) \approx -9.055`

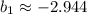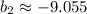
In consequence, the possible values of
`b` are -2.944 and -9.055, respectively.