Question

This is going to be my 13th reason please help me

Answer 1

The radius of these cylinders is approximately 1 foot.

Explanation:

According to this graph, the volume of the cylinder is directly proportional to its height, that is, radius remains constant. The expression of direct proportionality:

`V \propto h`

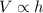
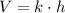`V = k\cdot h` (1)

Where:

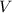`V` - Volume of the cylinder, in cubic feet.

`h` - Height of the cylinder, in feet.

`k` - Proportionality constant, in square feet.

Besides, the proportionality constant is described by this expression:

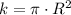`k = \pi \cdot R^(2)` (2)

Where
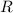`R` is the radius of the cylinder, in feet.

If we know that
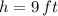`h = 9\,ft` and
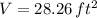`V = 28.26\,ft^(2)`, then the radius of the cylinder is:

`k = (V)/(h)`

`k = 3.14`

`R = \sqrt{(k)/(\pi) }`

`R \approx 1\,ft`

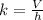
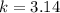
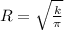
The radius of these cylinders is approximately 1 foot.