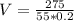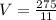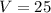Question

wind resistance varies jointly as an objects surface area and velocity. if an object traveling at 55 miles per hour with a surface area of 20 square feet experiences a wind resistance of 220 newtons how fast must a car with 55 square feet of surface area travel in order to experience a wind resistance of 275 newtons?​

Answer 1

25 miles per hour

Explanation:

Given

`W = Wind\ resistance`

`A = Surface\ Area`

`V = Velocity`

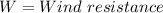
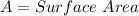
The joint variation can be represented as:

`W\ \alpha\ A*V`

Where:

`V = 55; A = 20; W = 220`

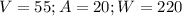
Required

Find V, when:
`A = 55; W = 275`

We have:

`W\ \alpha\ A*V`

Express as an equation

`W= k *A*V`

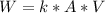
Where k is the constant of variation

Make k the subject

`k = (W)/(A*V)`

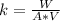
When:
`V = 55; A = 20; W = 220`

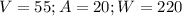
We have:

`k = (220)/(20 *55 )`

`k = (220)/(1100)`

`k = 0.2`

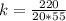
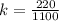
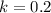
When:
`A = 55; W = 275`

We have:

`k = (W)/(A*V)`

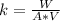
Substitute:
`A = 55; W = 275` and
`k = 0.2`

`0.2 = (275)/(55 * V)`

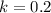
Make V the subject

`V= (275)/(55 * 0.2)`

`V= (275)/(11)`

`V= 25`