Answer:
If we want the greatest portion of pie, then you must choose the section with the greatest angle. Therefore, we must choose Section 2. But if we want the smallest portion of pie, then we must choose Section 1.
Explanation:
From statement, we know that measure of the angle ABC is equal to the sum of measures of angles ABD (section 1) and DBC (section 2), that is to say:
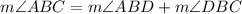 (1)
(1)
If we know that
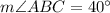 ,
,
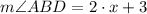 and
and
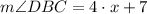 , then the value of
, then the value of
 is:
is:
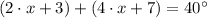
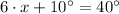
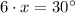
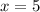
Then, we check the angles of each section:
Section 1
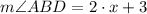
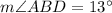
Section 2
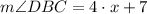
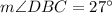
If we want the greatest portion of pie, then you must choose the section with the greatest angle. Therefore, we must choose Section 2. But if we want the smallest portion of pie, then we must choose Section 1.