Question

Assume we cut the last piece of the pie into two sections (1 and 2) along ray BD

such that m∠ABD = 2x+3, m∠CBD = 4x+7, and m∠ABC = 40°. Based on this information,
would you ask for section 1 or section 2 (you have to pick one) for dessert? Provide numerical evidence to back up your choice. Explain your reasoning and your methods.

Answer 1

If we want the greatest portion of pie, then you must choose the section with the greatest angle. Therefore, we must choose Section 2. But if we want the smallest portion of pie, then we must choose Section 1.

Explanation:

From statement, we know that measure of the angle ABC is equal to the sum of measures of angles ABD (section 1) and DBC (section 2), that is to say:

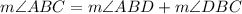`m \angle ABC = m\angle ABD + m\angle DBC` (1)

If we know that
`m\angle ABC = 40^(\circ)`,
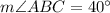`m\angle ABD = 2\cdot x + 3` and
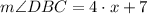`m\angle DBC = 4\cdot x + 7`, then the value of
`x` is:

`(2\cdot x + 3)+(4\cdot x + 7) = 40^(\circ)`

`6\cdot x +10^(\circ) = 40^(\circ)`

`6\cdot x = 30^(\circ)`

`x = 5`

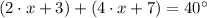
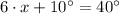
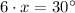
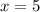
Then, we check the angles of each section:

Section 1

`m\angle ABD = 2\cdot x + 3`

`m\angle ABD = 13^(\circ)`

Section 2

`m\angle DBC = 4\cdot x + 7`

`m\angle DBC = 27^(\circ)`

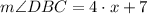
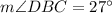
If we want the greatest portion of pie, then you must choose the section with the greatest angle. Therefore, we must choose Section 2. But if we want the smallest portion of pie, then we must choose Section 1.