Question

A sample of Xe gas is observed to effuse through a pourous barrier in 4.83 minutes. Under the same conditions, the same number of moles of an unknown gas requires 2.29 minutes to effuse through the same barrier. The molar mass of the unknown gas is _____ g/mol.​

Answer 1

28.93 g/mol

Step-by-step explanation:

This is an extension of Graham's Law of Effusion where
`(R1)/(R2) = \sqrt{(M2)/(M1) } = (t2)/(t1)`

We're only talking about molar mass and time (t) here so we'll just concentrate on
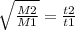`\sqrt{(M2)/(M1) } = (t2)/(t1)`. Notice how the molar mass and time are on the same position, recall effusion is when gas escapes from a container through a small hole. The time it takes it to leave depends on the molar mass. If the gas is heavy, like Xe, it would take a longer time (4.83 minutes). If it was light it would leave in less time, that gives us somewhat an idea what our element could be, we know that it's atleast an element before Xenon.

Let's plug everything in and solve for M2. I chose M2 to be the unknown here because it's easier to have it basically as a whole number already.

`\sqrt{(M2)/(131) } = (2.29)/(4.83)`

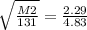
The square root is easier to deal with if you take it out in the first step, so let's remove it by squaring each side by 2, the opposite of square root essentially.

`(\sqrt{(M2)/(131) } )^2= ((2.29)/(4.83))^2`

`{(M2)/(131) } = (0.47)^2`

`{(M2)/(131) } = 0.22`

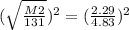
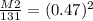
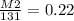
M2= 0.22 x 131

M2= 28.93 g/mol