Answer:
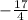 is 27th term of the given sequence.
is 27th term of the given sequence.
Explanation:
Given sequence is
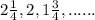
Here, first term of the sequence,
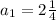
By subtracting first term from the second term of the sequence,
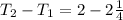
=
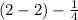
=
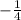
Similarly, difference in second and third term,
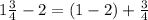
=
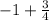
=
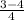
=
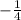
Therefore, there is a common difference (d) of
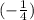 .
.
Hence, the sequence is an Arithmetic sequence.
Explicit formula of an Arithmetic sequence is given by,
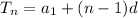
Here, n = number of term
If,
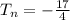
By substituting these values in the formula,


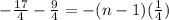
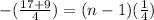
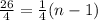
n - 1 = 26
n = 27
Therefore,
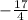 is 27th term of the given sequence.
is 27th term of the given sequence.