Answer:
B: 27
Explanation:
The total number of animals in a shelter is modeled by the function:

Where x is the number of cages at the facility.
We want to determine the number of cages if there are a total of 243 animals at the shelter.
So, we can set our function to 243 and solve for x:
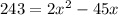
Subtract 243 from both sides:
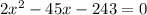
Solve the quadratic. Factoring and completing the square seems too difficult, so we can use the quadratic formula:
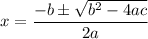
In this case, a = 2, b = -45, and c = -243. Substitute:
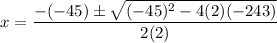
Evaluae:
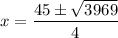
Evaluate:
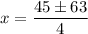
Therefore, our two solutions are:
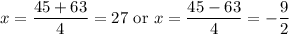
Since we cannot have negative or half a cage, we can ignore the second solution.
Therefore, there are a total of 27 cages at the shelter.
Our answer is B.