Question

9.Two cars have a rear-end collision. A 1200 kg Honda moving at 20 m/s strikes a 1000 kg Ford moving at 15

m/s. Their bumpers become locked and they continue to move as one mass. What is their final velocity?

Answer 1

The final velocity of the Honda-Ford system is 17.727 meters per second.

Step-by-step explanation:

According to the statement, there are no external forces acting on both cars, so there is an entirely inelastic collision between the Honda car and the Ford car, whose final velocity can be determined by solely using the Principle of Linear Momentum Conservation. A rear-end collision mean that both cars move in the same direction:

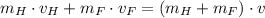`m_(H)\cdot v_(H) + m_(F)\cdot v_(F) = (m_(H)+m_(F))\cdot v` (1)

Where:

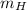`m_(H)` - Mass of the Honda car, in kilograms.

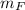`m_(F)` - Mass of the Ford car, in kilograms.

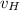`v_(H)` - Initial velocity of the Honda car, in meters per second.

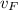`v_(F)` - Initial velocity of the Ford car, in meters per second.

`v` - Final velocity of the Honda-Ford system, in meters per second.

If we know that
`m_(H) = 1200\,kg`,
`m_(F) = 1000\,kg`,
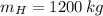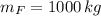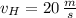`v_(H) = 20\,(m)/(s)` and
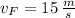`v_(F) = 15\,(m)/(s)`, then the final velocity of the Honda-Ford system is:

`m_(H)\cdot v_(H) + m_(F)\cdot v_(F) = (m_(H)+m_(F))\cdot v`

`v = (m_(H)\cdot v_(H)+m_(F)\cdot v_(F))/(m_(H)+m_(F))`

`v = 17.727\,(m)/(s)`

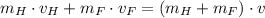
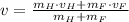
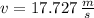
The final velocity of the Honda-Ford system is 17.727 meters per second.