Question

In a lab experiment, the decay of a radioactive isotope is being observed. At the

beginning of the first day of the experiment the mass of the substance was 500 grams
and mass was decreasing by 9% per day. Determine the mass of the radioactive
sample at the beginning of the 17th day of the experiment. Round to the nearest tenth
(if necessary).

Answer 1

Approximately 110.6 grams remain at the beginning of the 17th day.

Explanation:

At the beginning of the first day, the mass of the substance was 500 grams.

It decreases by 9% per day.

And we want to determine the mass of the sample at the beginning of the 17th day.

First, we need to find our ratio of decay. Since it decreases by 9% or 0.09 each day, the mass of the substance after each subsequent day will be 100% - 9% or 1 - 0.09 or 0.91 of the previous day.

We can write a exponential function to model this. An exponential function has the form:

`f(x)=ar^x`

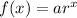
Where a is the initial term and r is the rate.

Let x represent the number of days after the first day. Substitute 500 for a and 0.91 for r:

`f(x)=500(0.91)^x`

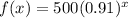
The 17th day is 16 days after the first day. So, the amount of mass remaining on the beginning of the 17th day is when x = 16. Substitute:

`f(x)=500(0.91)^(16)`

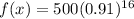
Approximate. Therefore:

`f(x)\approx110.6\text{ grams}`

Approximately 110.6 grams remain at the beginning of the 17th day.