Question

Find the absolute extrema of the given function: f(x)=x^4 − 3x^2 + 4, on the interval [−1,1]

Answer 1

The absolute maximum is 4, and the absolute minimum is 2.

Explanation:

We are given the function:

`f(x)=x^4-3x^2+4`

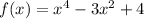
And we want to find the absolute extrema of the function on the interval [-1, 1].

So, we will find the smallest and largest y-value within the interval. First, we can evaluate the function at its endpoints. So:

`f(-1)=(-1)^4-3(-1)^2+4=2`

And:

`f(1)=(1)^4-3(1)^2+4=2`

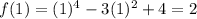
Our endpoints are (-1, 2) and (1, 2).

Recall that extrema only occurs at critical points. Critical points are where the derivative of the function equals 0. So, we can find the derivative of the function:

`\displaystyle f'(x)=(d)/(dx)\left[x^4-3x^2+4\right]`

Differentiate:

`f'(x)=4x^3-6x`

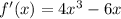
Set the function equal to 0:

`0=4x^3-6x`

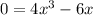
Solve for x. Factor:

`2x(2x^2-3)=0`

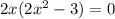
Zero Product Property:

`2x=0\text{ or } 2x^2-3=0`

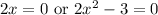
Solve for each case. Therefore:

`\displaystyle x=0\text{ or } x=\pm(\sqrt6)/(2)`

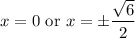
The second case is outside of our interval. So we can ignore it.

Evaluate the function at x = 0:

`f(0)=(0)^4-3(0)^2+4=4`

Therefore, for our function on the interval [-1, 1], the absolute maximum is 4, and the absolute minimum is 2.