Answer:
A. one B. (3, 4)
Explanation:
1. A good graph can answer both parts (see attached image).
2. Write equations for the two lines and find a simultaneous solution.
Line A: Slope from (2, 6) to (5, 0) is
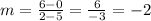
Using point-slope form
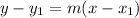
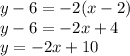
Line B: Slopt from (6, 6) to (0, 2) is
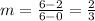
Using point-slope form, the equation for Line B is
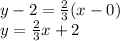
To find the simultaneous solution, set the y's equal.
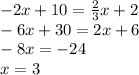
Find y using either equation to get y = 4.