Question

Which of the following equations could be solved to determine the length of RS?

Answer 1

`(Sin(80))/(RS) = (Sin(52.5))/(7)`

Explanation:

Given:

S = 52.5°

s = QR = 7

Q = 80°

q = RS = ?

Required:

Equation that could be used to find the length of RS

Solution:

We would need the law of Sines which is given as:

`(Sin(A))/(a) = (Sin(B))/(b) = (Sin(C))/(c)`

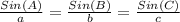
Applying the Law of Sines, we would have the following equation:

`(Sin(Q))/(q) = (Sin(S))/(s)`

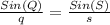
Plug in the values

`(Sin(80))/(RS) = (Sin(52.5))/(7)`

Therefore, the equation that can be used to determine the length of RS is
`(Sin(80))/(RS) = (Sin(52.5))/(7)`