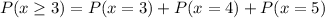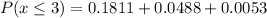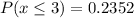Question

In a television series there is exactly one crime committed in every episode. It has been observed that the probability that the criminal is male in an episode is 0.35. What is the probability, rounded to three significant figures, that in five consecutive episodes the criminal is a male at least 3 times?

Answer 1

`P(x \le 3) = 0.2352`

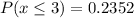
Explanation:

Given

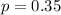`p = 0.35` --- male committing a crime in an episode

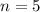`n = 5` -- Number of episodes

Required

Determine the probability of male committing a crime at least 3 times

This question illustrates binomial distribution and will be solved using;

`P(x) = ^nC_x * p^x * (1 - p)^{n-x`

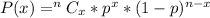
So, the required probability is represented as:

`P(x \ge 3)`

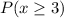
And will be calculated using:

`P(x \ge 3) = P(x = 3) + P(x = 4) + P(x = 5)`

`P(x = 3) = ^5C_3 * (0.35)^3 * (1 - 0.35)^(5-3)`

`P(x = 3) = ^5C_3 * (0.35)^3 * (1 - 0.35)^2`

`P(x = 3) = 10 * (0.35)^3 * (0.65)^2`

`P(x = 3) = 0.1811`

`P(x = 4) = ^5C_4 * (0.35)^4 * (1 - 0.35)^(5-4)`

`P(x = 4) = 5 * (0.35)^4 * (1 - 0.35)^1`

`P(x = 4) = 5 * (0.35)^4 * (0.65)`

`P(x = 4) = 0.0488`

`P(x = 5) = ^5C_5 * (0.35)^5 * (1 - 0.35)^(5-5)`

`P(x = 5) = 1 * (0.35)^5 * (1 - 0.35)^0`

`P(x = 5) = 1 * (0.35)^5 * (0.65)^0`

`P(x = 5) = 1 * (0.35)^5 * 1`

`P(x = 5) = 0.0053`

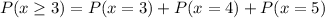
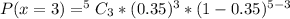
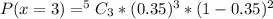
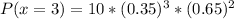
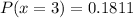
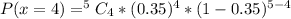
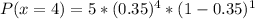
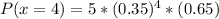
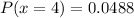
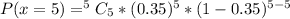
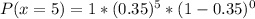
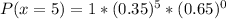
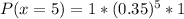
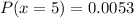
So:

`P(x \ge 3) = P(x = 3) + P(x = 4) + P(x = 5)`

`P(x \le 3) = 0.1811 + 0.0488 + 0.0053`

`P(x \le 3) = 0.2352`