Answer:
The ratio of the volume of the triangular prism to the volume of the cuboid is
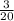 .
.
Explanation:
Geometrically speaking, the volume of the prism is equal to the product of the area of the base and its height. Then, the volumes of the triangular prism and the cuboid are, respectively:
Triangular prism
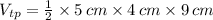
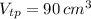
Cuboid
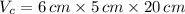
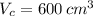
Lastly, the ratio of the volume of the triangular prism to the volume of the cuboid is:
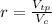
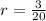
The ratio of the volume of the triangular prism to the volume of the cuboid is
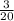 .
.