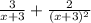Answer:
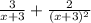
Explanation:
Given
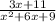
Required
Express as partial fraction
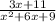
Expand the numerator
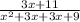
Factorize
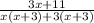
Factor out x + 3
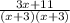
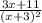
As a partial fraction, we have:
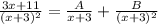
Take LCM
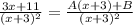
Cancel out (x + 3)^2 on both sides
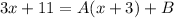
Open bracket
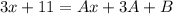
By comparison, we have:
 ===>
===>
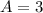
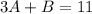
Substitute 3 for A
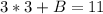
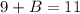
Solve for B
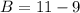
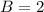
Substitute:
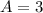 and
and
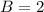 in
in
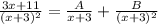
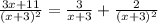
Hence, the partial fraction is: