Question

A bicycle rider pushes a 13kg bicycle up a steep hill. the incline is 24 degree and the road is 275m long. the rider pushes the bike parallel to the road with a force of 25N.

A. How much work does the rider do on the bike?
B. How much work is done by the force of gravity on the bike?

Answer 1

A. W = 6875.0 J.

B. W = -14264.6 J.

Step-by-step explanation:

A. The work done by the rider can be calculated by using the following equation:

`W_(r) = |F_(r)|*|d|*cos(\theta_(1))`

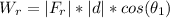
Where:

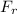`F_(r)`: is the force done by the rider = 25 N

d: is the distance = 275 m

θ: is the angle between the applied force and the distance

Since the applied force is in the same direction of the motion, the angle is zero.

`W_(r) = |F_(r)|*|d|*cos(0) = 25 N*275 m = 6875.0 J`

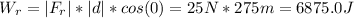
Hence, the rider does a work of 6875.0 J on the bike.

B. The work done by the force of gravity on the bike is the following:

`W_(g) = |F_(g)|*|d|*cos(\theta_(2))`

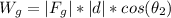
The force of gravity is given by the weight of the bike.

`F_(g) = -mgsin(24)`

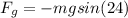
And the angle between the force of gravity and the direction of motion is 180°.

`W_(g) = |mgsin(24)|*|d|*cos(\theta_(2))`

`W_(g) = 13 kg*9.81 m/s^(2)*sin(24)*275 m*cos(180) = -14264.6 J`

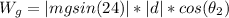
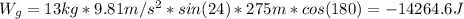
The minus sign is because the force of gravity is in the opposite direction to the motion direction.

Therefore, the magnitude of the work done by the force of gravity on the bike is 14264.6 J.

I hope it helps you!