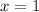Translate to a quadratic equation, then solve using the quadratic formula. A positive integer squared plus 5 times its consecutive integer is equal to 11. Find the integers.

Question

asked Jul 4, 2022 207k views

1 Answer

Achwilko · Answer 1 · 2022-07-10T11:42:57+0000

Answer:

The integer is 1

Explanation:

Required

Translate and solve

Let the positive integer be x.

So, we have;

The square of the integer is: x^2

Plus 5 times its consecutive integer is: x^2 + 5(x + 1)

Equals 11 is: x^2 + 5(x + 1) = 11

So, we have:

x^2 + 5(x + 1) = 11

Open bracket

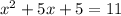
x^2 + 5x + 5= 11

Subtract 11 from both sides

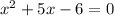
x^2 + 5x -6= 0

Expand

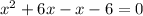
x^2 + 6x - x-6= 0

Factorize:

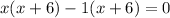
x(x + 6) - 1(x+6)= 0

Factor out x + 6

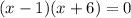
(x - 1) (x+6)= 0

Split

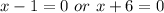
$x - 1 = 0\ or\ x + 6 = 0$

Solve for x in both cases

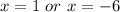
$x = 1\ or\ x = -6$

Since the number is positive, then
x = 1