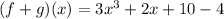Question

If f(x) = 3x + 10 and g(x) = 2x - 4, find (f+ g)(x).

O A. (f+ g)(x) = 3x + 2x + 6
O B. (f+ g)(x) = -3x - 2x - 14
O C. (f+ g)(x) = 3x - 2x + 14
O D. (f+ g)(x) = 5x + 6

Answer 1

the answer is B

Explanation:

Answer 2

So the correct answer is:

`\( (f + g)(x) = 3x^3 + 2x + 6 \)`

Option A.

To find
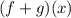`\( (f + g)(x) \)`, you simply add the functions f(x) and g(x) together. Here's how you do it step by step:

1. Write down the given functions:

`\( f(x) = 3x^3 + 10 \)`

`\( g(x) = 2x - 4 \) \lim_(n \to \infty) a_n`

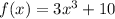
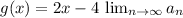
2. Add the functions together by combining like terms:

`\( (f + g)(x) = f(x) + g(x) \)`

`\( (f + g)(x) = (3x^3 + 10) + (2x - 4) \)`

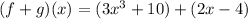
3. Simplify the expression by adding the constants and keeping the other terms separate since they are not like terms:

`\( (f + g)(x) = 3x^3 + 2x + 10 - 4 \)`

`\( (f + g)(x) = 3x^3 + 2x + 6 \)`