(Простите, пожалуйста, мой английский. Русский не мой родной язык. Надеюсь, у вас есть способ перевести это решение. Если нет, возможно, прилагаемое изображение объяснит достаточно.)
Use the shell method. Each shell has a height of 3 - 3/4 y ², radius y, and thickness ∆y, thus contributing an area of 2π y (3 - 3/4 y ²). The total volume of the solid is going to be the sum of infinitely many such shells with 0 ≤ y ≤ 2, thus given by the integral
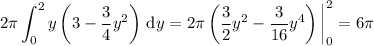
Or use the disk method. (In the attachment, assume the height is very small.) Each disk has a radius of √(4/3 x), thus contributing an area of π (√(4/3 x))² = 4π/3 x. The total volume of the solid is the sum of infinitely many such disks with 0 ≤ x ≤ 3, or by the integral
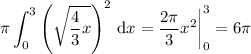
Using either method, the volume is 6π ≈ 18,85. I do not know why your textbook gives a solution of 90,43. Perhaps I've misunderstood what it is you're supposed to calculate? On the other hand, textbooks are known to have typographical errors from time to time...