Given:
The given function is:
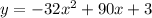
To find:
The range of the given function.
Solution:
We have,
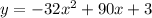
It is a quadratic function because the highest power of the variable x is 2.
Here, the leading coefficient is -32 which is negative. So, the graph of the given function is a downward parabola.
If a quadratic function is
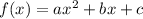 , then the vertex of the quadratic function is:
, then the vertex of the quadratic function is:
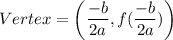
In the given function,
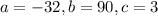 .
.
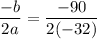
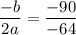
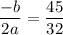
The value of the given function at
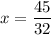 is:
is:
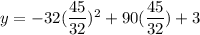
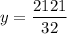
The vertex of the given downward parabola is
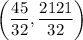 . It means the maximum value of the function is
. It means the maximum value of the function is
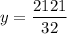 . So,
. So,
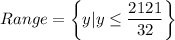
![Range=\left(-\infty, (2121)/(32)\right ]](https://img.qammunity.org/2022/formulas/mathematics/high-school/cpvsfq6gng84o63mm4419ymoeuav33cgj5.png)
Therefore, the range of the given function is
![\left (-\infty, (2121)/(32)\right ]](https://img.qammunity.org/2022/formulas/mathematics/high-school/71xgp79deo07bclt86r8fgy3h4k8fngd0a.png) .
.