Answer:
Angular velocity:
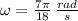 (
(
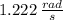 )
)
Linear velocity:
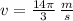 (
(
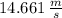 )
)
Explanation:
The gear experiments a pure rotation with axis passing through its center, the angular (
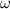 ), in radians per second, and linear velocities (
), in radians per second, and linear velocities (
 ), in inches per second, of a point on the outer edge of the element are, respectively:
), in inches per second, of a point on the outer edge of the element are, respectively:
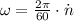 (1)
(1)
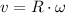 (2)
(2)
Where:
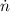 - Rotation rate, in revolutions per minute.
- Rotation rate, in revolutions per minute.
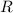 - Radius of the gear, in inches.
- Radius of the gear, in inches.
If we know that
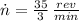 and
and
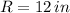 , then the linear and angular velocities of the gear are, respectively:
, then the linear and angular velocities of the gear are, respectively:
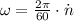
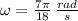 (
(
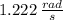 )
)
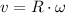
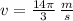 (
(
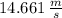 )
)