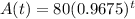Answer:
The percentage rate of decay per year is of 3.25%.
The function showing the mass of the sample remaining after t is
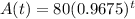
Explanation:
Equation for decay of substance:
The equation that models the amount of a decaying substance after t years is given by:
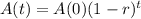
In which A(0) is the initial amount and r is the decay rate, as a decimal.
Every 21 years, its mass decreases by half.
This means that
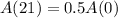 . We use this to find r, the percentage rate of decay per year.
. We use this to find r, the percentage rate of decay per year.
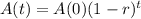
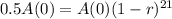
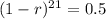
![\sqrt[21]{(1-r)^(21)} = \sqrt[21]{0.5}](https://img.qammunity.org/2022/formulas/mathematics/college/36c20hropm0lsqyd8138nsjhdhr5u5a474.png)
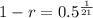
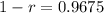
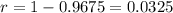
The percentage rate of decay per year is of 3.25%.
Given that the initial mass of a sample of Element X is 80 grams.
This means that

The equation is:
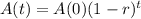
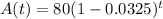
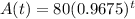
The function showing the mass of the sample remaining after t is