Question

A cylinder has a helght of 16 cm and a radius of 5 cm. A cone has a helght of 12 cm and a radius of 4 cm. If the cone is placed inside the cylinder

as shown, what is the volume of the alr space surrounding the cone Inside the cylinder? (Use 3.14 as an approximation of pl.)
OA 452.16 cm
OB.
840.54 cm
OC 1,055.04 cm
OD. 1,456.96 cm

Answer 1

1055.04 cm³

Explanation:

Given that,

Height of a cylinder, h = 16 cm

Radius of the cylinder, r = 5 cm

The height of a cone, h' = 12 cm

The radius of a cone, r' = 4 cm

The volume of the cylinder will be :

`V=\pi r^2 h\\\\=3.14* 5^2* 16\\\\=1256\ cm^3`

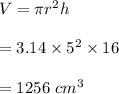
The volume of a cone is given by :

`V'=(1)/(3)\pi r^2 h\\\\=(1)/(3)* 3.14* (4)^2* 12\\\\=200.96\ cm^3`

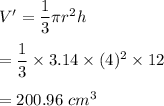
Volume of the air surrounding the cone Inside the cylinder = 1256 - 200.96 = 1055.04 cm³

Hence, the required answer is equal to 1055.04 cm³.