Answer:
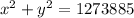
Explanation:
Given
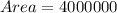
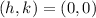
Required
The equation of the circle
First, we calculate the radius of the circle using;
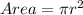
This gives:
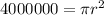
Divide both sides by


Take
 as 3.14
as 3.14
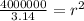
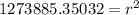
Approximate
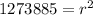
Rewrite as:
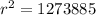
The equation of the circle is:
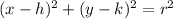
Where:
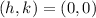
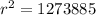
So, we have:
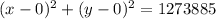
Open brackets
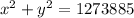
(c) is correct.
The difference in
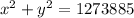 and (c) in the question is due to approximation
and (c) in the question is due to approximation