Question

An automobile manufacturer has developed a new compact automobile. A random sample of 64 of the new automobiles showed that the automobiles had a sample mean mileage of 28.75 miles per gallon and a sample standard deviation of 3.4 miles per gallon. a) Find the 95% confidence interval for the population mean mileage, and state your conclusion. b) Find the 98% confidence interval for the population mean mileage, and state your conclusion.

Answer 1

The 95% confidence interval for the population mean mileage is

(27.917, 29.593)

The 98% confidence interval for the population mean mileage

(27.737, 29.762)

Explanation:

Step(i):-

Given that the random sample size 'n' = 64

Given that the mean of sample x⁻ = 28.75miles

Given that the standard deviation of the sample (S) = 3.4 miles

Degrees of freedom = n-1 = 64-1 =63

t₀.₀₅ = 1.9983

Step(ii):-

95% confidence interval for the population mean mileage is determined by

`(x^(-) - t_(0.05) (S)/(√(n) ) , x^(-) + t_(0.05) (S)/(√(n) ))`

`(28.75-1.99(3.4)/(√(64) ),28.75 + 1.99 (3.4)/(√(64) ) )`

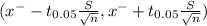
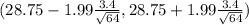
(28.75 - 0.845 , 28.75 + 0.845)

(27.917 , 29.593)

Step(iii):-

98% confidence interval for the population mean mileage is determined by

`(x^(-) - t_(0.02) (S)/(√(n) ) , x^(-) + t_(0.02) (S)/(√(n) ))`

`(28.75-2.3824(3.4)/(√(64) ),28.75 + 2.3824 (3.4)/(√(64) ) )`

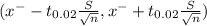
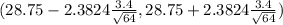
(28.75 - 1.01252 , 28.75 + 1.01252)

(27.737 , 29.762)

Final answer:-

98% confidence interval for the population mean mileage is

(27.737 , 29.762)