Answer:
The value of the test statistic is z = -4.19.
Explanation:
The test statistic is:

In which X is the sample mean,
 is the expected value for the population mean,
is the expected value for the population mean,
 is the standard deviation and n is the size of the sample.
is the standard deviation and n is the size of the sample.
Average 13.5 years of experience in their specialties, with a standard deviation of 7.6 years.
This means that
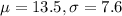
A random sample of 150 doctors from HMOs shows a mean of only 10.9 years of experience.
This means that
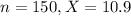
What is the test statistic?


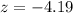
The value of the test statistic is z = -4.19.