Answer:
the bus can travel 24.54 km before the flywheel has to be spun up to speed again
Step-by-step explanation:
Given the data in the question;
mass of wheel m = 1600 kg
radius of the fly wheel r = 0.650 m
angular speed of the wheel ω = 4000 rev/min = 418.879 rad/s
Average speed of the bus v = 40 km/h = 11.1111 m/s
Power p = 18 hp = 13428 watt
So moment of inertia of the fly wheel is;
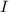 =
=
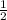 mr²
mr²
we substitute
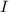 =
=
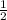 × 1600 kg × (0.650 m)²
× 1600 kg × (0.650 m)²
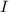 = 338 kgm²
= 338 kgm²
So, the rotational energy of the bus will be;
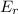 =
=
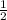
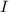 ω²
ω²
we substitute
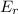 =
=
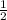 × 338 kgm² × ( 418.879 rad/s )
× 338 kgm² × ( 418.879 rad/s )
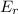 = 29652675.212329 J
= 29652675.212329 J
relation of power to energy
P = E / t
but we know that time t = distance / velocity
t = d/v
∴
P = E / ( d/v)
we solve for distance (d)
P = Ev / d
Pd = Ev
d = Ev / P
so we substitute
d = [( 29652675.212329 J )( 11.1111 m/s )] / [ 13428 W ]
d = 24536.33 m
d = 24.54 km
Therefore, the bus can travel 24.54 km before the flywheel has to be spun up to speed again