Solution :
The PV "perpetual" obligation of the firm =
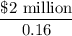
= $ 12.5 million
Also based on duration of the perpetuity, duration of this obligation =
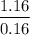
= 7.25 years
Let
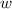 be the
be the
 on the
on the
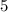 year maturity bond, which has a duration of
year maturity bond, which has a duration of
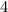 years. Then :
years. Then :
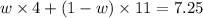
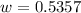
Therefore,
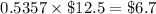 million in the
million in the
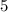 year bond
year bond
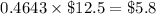 million in the
million in the
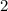 year bond.
year bond.
Therefore, the total invested amounts to $
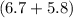 million =
million =
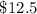 million, which fully matches the funding needs.
million, which fully matches the funding needs.