Question

Halcrow Yolles purchased equipment for new highway construction in Manitoba, Canada, costing $500,000 Canadian. The estimated salvage at the end of the expected life of 5 years is $50,000. Various acceptable depreciation methods are being studied currently. Determine the depreciation for year 2 using the DDB(Double Declining Balance), 150% DB(Declining Balance), and SL(Straight Line Depreciation) methods.

Answer 1

Method I : SL method

Cost of equipment = $ 500,000

Salvage value = $ 50,000

Expected life = 5 years

Depreciation =
`$\frac{\text{(cost of equipment - salvage value)}}{\text{expected life}}$`

`$=((500,000-50,000))/(5)$`

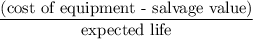
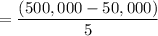
= 90,000

Therefore, the
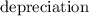`$\text{depreciation}$` is $ 90,000 using the SL method.

Method II : DDB method

Cost of equipment = $ 500,000

Expected life = 5 years

So, calculating the
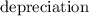`$\text{depreciation}$` at the end of the year 1 is :

Depreciation =
`$\text{cost of equipment }* \frac{2}{\text{expected life}}$`

`$=500,000* (2)/(5)$`

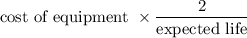
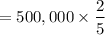
= $ 200,000

So the book value at the end of the year 1 = $ 500,000 - $ 200,000

= $ 300,000

Now calculating the
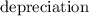`$\text{depreciation}$` at the end of the year 2 is :

Depreciation =
`$\text{book value at the end of year 1 }* \frac{2}{\text{expected life}}$`

`$=300,000* (2)/(5)$`

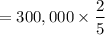
= $ 120,000

Therefore, the
`$\text{depreciating}$` value is $ 120,000 using the DDB method.

Method III : 150% DB method

Cost of equipment = $ 500,000

Expected life = 5 years

So, calculating the depreciation in year 1 is :

Depreciation =
`$\text{cost of equipment }* \frac{1.5}{\text{expected life}}$`

`$=500,000* (1.5)/(5)$`

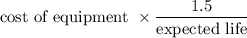
= $ 150,000

So the book value at the end of the year 1 = $ 500,000 - $ 150,000

= $ 350,000

Now calculating the depreciation in year 2 is :

Depreciation =
`$\text{book value at the end of year 1 }* \frac{1.5}{\text{expected life}}$`

`$=350,000* (1.5)/(5)$`

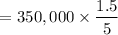
= $ 105,000

Therefore, the
`$\text{depreciating}$` value is $ 105,000 using the 150% DB method.