Question

It is known that the straight line l is tangent to the circle x^2+y^2=4 at a point on the x-axis, and intersects with the straight line y=(1/2)x at the point P, find the coordinates of the point P​

Answer 1

Explanation:

The general equation of a circle is

`(x \ - \ h)^2 \ + \ (y \ - \ k)^2 \ = \ r^(2)`,

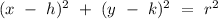where h and k forms the coordinates of the centre of the circle.

When the circle has a centre at the origin, the equation reduces into

.
`x^2 \ + \ y^2 \ = r^2`.

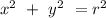Now, we are interested in solving for the x-intercepts (the x-coordinates when the circle intersects the x-axis), of the circle

`x^2 \ + \ y^2 \ = \ 4` .

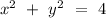Thus,

`x^2 \ + \ (0)^2 \ = \ 4 \\ \\ \\ \-\hspace{1.3cm} x^(2) \ = \ 4 \\ \\ \\ \-\hspace{1.4cm} x \ = \ \pm \ 2`.

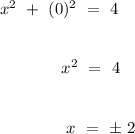Geometrically speaking, the tangent to the circle at the point defined by one of the x-intercepts of the circle is actually a vertical line, more specifically the lines
`x \ = \ \pm \ 2`.

First and foremost, for the vertical line
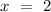`x \ = \ 2`, it intersects the straight line
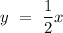`y \ = \ \displaystyle(1)/(2)x` , giving the y-coordinate for point P,

`y \ = \ \displaystyle(1)/(2)(2) \\ \\ \\ y \ = \ 1`.

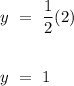Hence, the coordinates of point P are
`(1, \ 1)`.

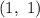However, since there are no boundaries given in the question and a circle is symmetrical about its centre, thus, point P also exists when the vertical line
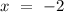`x \ = \ -2` and interdects the straight line
`y \ = \ \displaystyle(1)/(2)x`.

`y \ = \ \displaystyle(1)/(2)(-2) \\ \\ \\ y \ = \ -1`.

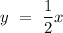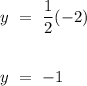Therefore, the coordinates of point P are also
`(1, \ -1)`.