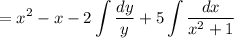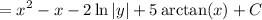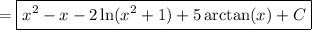Simplify the integrand as
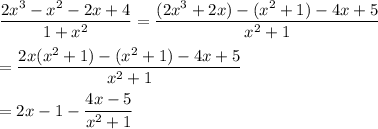
(in other words, compute the quotient and remainder)
We can further split up and prepare the remainder term for integration by rewriting it as
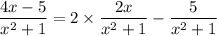
Now we integrate:
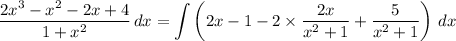

In the first remaining integral, substitute y = x² + 1 and dy = 2x dx. In the last integral, recall that d/dx [arctan(x)] = 1/(x² + 1).